如图所示，在竖直平面内有一金属环，环半径为0.5m，金属环总电阻为2Ω，在整个竖直平面内存在垂直纸面向里的匀强磁场，磁感应强度为B=1T，在环的最高点上方A点用铰链连接一长度为1.5m，

问题描述：

如图所示，在竖直平面内有一金属环，环半径为0.5m，金属环总电阻为2Ω，在整个竖直平面内存在垂直纸面向里的匀强磁场，磁感应强度为B=1T，在环的最高点上方A点用铰链连接一长度为1.5m，电阻为3Ω的导体棒AB，当导体棒AB摆到竖直位置时，导体棒B端的速度为3m/s．已知导体棒下摆过程中紧贴环面且与金属环有良好接触，则导体棒AB摆到竖直位置时AB两端的电压大小为（　　）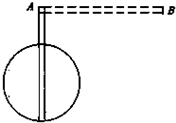

A. 0.4V

B. 0.65V

C. 2.25V

D. 4.5V

---

最佳答案：

当导体棒摆到竖直位置时，由v=ωr可得：C点的速度为：
vC=

1

3

vB=

1

3

×3m/s=1m/s
AC间电压为：UAC=EAC=BLAC•

vC

2

=1×0.5×

1

2

=0.25V
CB段产生的感应电动势为：ECB=BLCB•

vC+vB

2

=1×1×

1+3

2

=2V
圆环两侧并联，电阻为：R=

1

2

Ω=0.5Ω，
金属棒CB段的电阻为：r=2Ω
则CB间电压为：UCB=

R

r+R

ECB=

0.5

0.5+2

×2V=0.4V
故AB两端的电压大小为：UAB=UAC+UCB=0.25+0.4=0.65V
故选：B