如图所示，足够长的木板C放在光滑水平面上，长木板上面放置两个可视为质点的木块A、B，A、B与长木板间的动摩擦因数相同均为μ=0.2，A、B、C的质量分别是mA=mB=mC=0.2kg，开始时A、B、C

问题描述：

如图所示，足够长的木板C放在光滑水平面上，长木板上面放置两个可视为质点的木块A、B，A、B与长木板间的动摩擦因数相同均为μ=0.2，A、B、C的质量分别是m_A=m_B=m_C=0.2kg，开始时A、B、C都处于静止状态．某时刻同时对A、B施加方向相反的恒力F₁、F₂，F₁=1.0N，F₂=0.6N，经过t=1.0s的时间，同时撤去这两个力，（取g=10m/s²）问：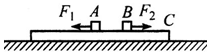

（1）在对A、B施加F₁、F₂作用的过程中，木板C的运动状态应该怎样，请说明理由；
（2）撤去F₁、F₂的瞬间，木块A、B的速度分别多大？
（3）经一定时间后A、B、C速度相同，其共同速度多大？

---

最佳答案：

（1）A、B对木板C的滑动摩擦力的大小相等，方向相反，所以在对A、B施加F1、F2作用的过程中，木板C保持静止．   
（2）在对A、B施加F1、F2作用的过程中，A、B的加速度分别为：
  aA=

F1-μmAg

mA

=

1-0.2×0.2×10

0.2

=3m/s2．
  aB=

F2-μmBg

mB

=

0.6-0.2×0.2×10

0.2

=1m/s2
同时撤去这两个力后，木块A、B的速度分别为
vA=aAt=3×1=3m/s
vB=aBt=1×1=1m/s
（3）取向左为正方向，由动量守恒定律得：mAvA-mBvB=（mA+mB+mC）v      
得 v=

2

3

（m/s）   
答：（1）在对A、B施加F1、F2作用的过程中，木板C保持静止；
（2）撤去F1、F2的瞬间，木块A、B的速度分别为3m/s和1m/s；
（3）经一定时间后A、B、C速度相同，其共同速度是

2

3

m/s．