问题描述：
如图所示，在竖直空间建立直角坐标系xOy，在第一象限和第四象限内存在竖直向上的，电场强度大小为E1的匀强电场和大小、方向均未知的匀强电场B1，在第二、三象限内存在水平向右，电场强度大小为E2的匀强电场和方向水平向里、磁感应强度的大小为B2的匀强电场．在x轴上坐标为（-d，0）的P点使一质量为m、电荷量为q的带正电的小球以某一速度v沿x轴成37°角的方向射出，小球恰好沿PQ方向匀速运动到y轴上的Q点，该小球进入到第一象限后做匀速圆周运动，恰好经历半个圆周到达半径为r的| 1 |
| 4 |
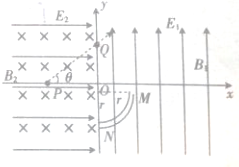
（1）E1与E2的大小之比．
（2）磁场B1的磁感应强度的大小和方向．
（3）小球从P点运动到N点所用的时间．
最佳答案： 
（1）在第二象限内的匀速直线运动可知，小球的重力电场力和洛伦兹力三力平衡，如图有：
故有：E2q=mgtan37°…①
小球进入到第一象限后做匀速圆周运动，故有：
mg=E1q…②
联立解得：
| E1 |
| E2 |
| 1 |
| tan37° |
| 4 |
| 3 |
（2）小球进入到第一象限后做匀速圆周运动，轨迹如下图，
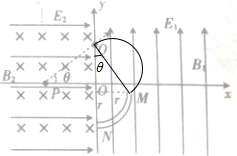由几何关系得：轨道半径满足：sin37°=| r |
| 2R |
由洛伦兹力提供向心力得：B1qv=
| mv2 |
| R |
由③④解得：B1=
| 6mv |
| 5qr |
由于粒子带正电，结合运动轨迹及左手定则可得，磁场B1的方向垂直于纸面向外．
（3）粒子从P到Q的时间为：t1=
| d |
| vcos37° |
做半圆运动的时间为：t2=
| πR |
| v |
做四分之一圆周运动的时间为：t3=
| πr |
| 2v |
总时间为t=t1+t2+t3…⑨
联立③⑥⑦⑧⑨得：t=
| 15d+16πr |
| 12v |
答：（1）E1与E2的大小之比为
| 4 |
| 3 |
（2）磁场B1的磁感应强度的大小为
| 6mv |
| 5qr |
（3）小球从P点运动到N点所用的时间为
| 15d+16πr |
| 12v |
