问题描述:
如图所示,在第一象限内,有垂直纸面向里的匀强磁场(磁场足够大),磁感应强度为B.一电子从O点沿纸面以速度v射入磁场中,速度方向与x轴成30°角,已知电子质量为m,电量为e.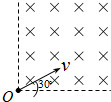
(1)定性地画出电子在磁场中的轨迹;求电子的轨道半径r;
(2)求电子离开磁场的出射点到O点的距离;
(3)求电子在磁场中运动的时间.
(1)由左手定则可知,粒子受力方向垂直速度方向向右下方,则可知运动轨迹如图: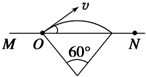
对电子在做圆周运动的过程中,设半径为r,有:
qvB=m
| v2 |
| r |
所以:
r=
| mv |
| eB |
(2)由1中所画图象,由几何关系可解得圆心角为60°,
由几何关系可知射出点到O点的距离等于电子的运动半径为
| mv |
| eB |
(3)电子在磁场中的运动周期T为:
T=
| 2πr |
| v |
电子在磁场中运动的圆心角为60°,则运动的时间为:
t=
| ||
| 2π |
联立解得:
t=
| πm |
| 3eB |
答:(1)轨迹如图所示;半径大小为
| mv |
| eB |
(2)电子从磁场中射出时距O点
| mv |
| eB |
(3)电子在磁场中运动的时间为
| πm |
| 3eB |

