如图所示，是一种古代配重式投石机的简易示意图，A端下落至杆与水平方向成θ=53°时，可将装在B处斗内的石块抛射出去．若已知石块抛出时配重物下落的竖直速度vA=15m/s，LA=2.5m，LB=10m，

问题描述：

如图所示，是一种古代配重式投石机的简易示意图，A端下落至杆与水平方向成θ=53°时，可将装在B处斗内的石块抛射出去．若已知石块抛出时配重物下落的竖直速度v_A=15m/s，L_A=2.5m，L_B=10m，忽略空气阻力影响，g取10m/s²，则（　　）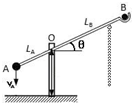

A. 石块从斗内射出时的速度约为v_B=14.4m/s

B. 石块从斗内射出时的速度约为v_B=30m/s

C. 石块的射程可达120m左右

D. 石块的射程可达45m左右

---

最佳答案：

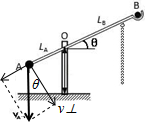
A、A端的速度可以分解为沿杆方向的分速度和垂直于杆的分速度，如图，则：v⊥=vAcos53°=15×

3

5

=9m/s

A端与B端的角速度相等，由v=ωr，可得B点的速度：vB=

v⊥

LA

•LB=

9

2.5

×10=36m/s．故A错误，B正确；
C、B点的高度约为：H=(LA+LB)sin53°=(2.5+10)×

4

5

=10m
竖直方向的分速度：v1=v•cos53°=36×

3

5

=21.6m/s
石块运动的时间为t，则：H=-v1t+

1

2

gt2
代入数据，得：t≈4.5s
水平方向的分速度：vs=v•sin53=36×

4

5

=28.8m
水平射程：x=vs•t=28.8×4.5=129.6m．故C正确，D错误．
故选：BC