问题描述:
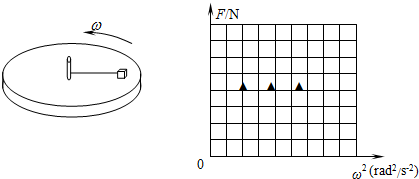
如图所示,与轻绳相连的滑块置于水平圆盘上,绳的另一端固定于圆盘中心的转轴上,绳子刚好伸直且无弹力,绳长r=0.5m,滑块随圆盘一起做匀速圆周运动(二者未发生相对滑动),滑块的质量m=1.0kg,与水平圆盘间的动摩擦因数μ=0.2,设最大静摩擦力等于滑动摩擦力,取g=10m/s2.求:(1)圆盘角速度ω1=1rad/s时,滑块受到静摩擦力的大小;
(2)圆盘的角速度ω2至少为多大时,绳中才会有拉力;
(3)画出圆盘角速度ω由0缓慢增大到4rad/s时,轻绳上的拉力F与角速度ω2的图象(绳未断).
(1)静摩擦力提供向心力,有:f=m
| ω | 21 |
代入数据解得:f1=0.5N;
(2)当静摩擦力达到最大值时,绳中才出现拉力,最大静摩擦力提供向心力,有:
μmg=m
| ω | 22 |
代入数据解得:ω2=2rad/s;
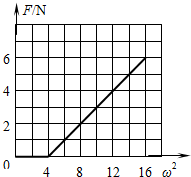
(3)当加速度 0≤ω≤2rad/s时,绳拉力 F=0
当2rad/s<ω≤4rad/s时,根据牛顿第二定律有:
F+μmg=mω2r,
解得绳中拉力:F=0.5ω2-2.
图象如图所示.
答:(1)圆盘角速度ω1=1rad/s时,滑块受到静摩擦力的大小为0.5N;
(2)圆盘的角速度ω2至少为2rad/s时,绳中才会有拉力;
(3)如图所示.

