如图所示，14竖直圆弧轨道与水平板组合成一体，其质量M=4kg，半径R=0.25m，一轻质弹簧右端固定在平板上，弹簧的原长正好等于水平板的长度．组合体放在水平地面上并与左侧竖直墙壁紧挨

问题描述：

如图所示，

1

4

竖直圆弧轨道与水平板组合成一体，其质量M=4kg，半径R=0.25m，一轻质弹簧右端固定在平板上，弹簧的原长正好等于水平板的长度．组合体放在水平地面上并与左侧竖直墙壁紧挨在一起．将质量m=1kg的小物块（可视为质点）从圆弧轨道上端以初速度v₀=2m/s释放，物块到达圆弧轨道最低点时与弹簧接触并压缩弹簧．已知小物块与水平板间的动摩擦因数μ=0.2，弹簧的最大压缩量x=0.2m，其它接触面的摩擦均不计，重力加速度g取10m/s²．求：

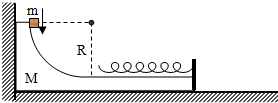
（1）小物块到达圆弧轨道最低点时对轨道的压力；
（2）弹簧的最大弹性势能．

---

最佳答案：

（1）小物块从圆弧轨道上端到圆弧轨道最低点的过程机械能守恒，则有：
 

1

2

mv02+mgR=

1

2

mv2
小物块到达圆弧轨道最低点时，由牛顿第二定律有：FN-mg=m

v2

R

联立解得 FN=46N
根据牛顿第三定律，小物块对轨道的压力FN′=46N，竖直向下．
（2）自小物块接触弹簧到弹簧压缩最短的过程中，取向右为正方向，小物块、弹簧、组合体组成的系统：
由动量守恒定律得 mv=（m+M）v′
由能量守恒定律得 

1

2

mv2=

1

2

(m+M)v′2+Q+EP
又 Q=μmgx
解得：Ep=3.2J
答：
（1）小物块到达圆弧轨道最低点时对轨道的压力大小为46N，方向竖直向下；
（2）弹簧的最大弹性势能是3.2J．