问题描述:
如图所示,质量分别为m、2m的物体a、b通过轻绳和不计摩擦的定滑轮相连,均处于静止状态,a与水平面上固定的劲度系数为k的轻质弹簧相栓连,Q点有一挡板,若有物体与其垂直相撞会以原速率弹回,现剪断a、b之间的绳子,a开始上下往复运动,b下落至P点时以原速率水平向右运动,当b静止时,a恰好首次到达最低点,一直PQ长s0,重力加速度g,b距P高h,且仅经过P点一次,b滑动时动摩擦因数μ,a、b均可看做质点,弹簧在弹性限度范围内,试求: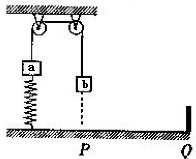
(1)物体a的最大速度;
(2)物体a第一次运动到最低点所需要的时间;
(3)物体b停止的位置与P点距离.
= (1)没有间断细线前,对a,由平衡条件得:2mg=mg+kx1,当弹簧弹力与a的重力相等时a的速度最大,由平衡条件得:mg=kx2,解得:x1=x2=mgk,初速度位置与速度最大位置弹簧的弹性势能EP相等,由机械能守恒定律得:EP+...

